基于 GA 遗传算法的智能组题模块的设计与应用

作者：南侠 (opens new window)，编程导航星球 (opens new window) 编号 29240

基于 PyGad + Flask 的遗传算法实现的智能题单生成项目，根据题单题目难度分布、题目类型分布、受众能力等参数得到最优题目组合方案

在OJ系统中，题单生成是一个至关重要的环节。

一般来说，题单由多道题目组合而成，以满足特定需求，如受众能力、题型分布、难度比例和知识点分布等。

然而，传统的方法往往依赖于经验，通过筛选和组合题目来达到预期目标。

但这种方法存在时间成本高、误差率大的问题，对于新手来说尤其不友好。

因此，本文提出了一种新的思路：利用GA遗传算法来解决这一问题。通过将各种因素作为适应度函数的组成参数，在经过多次遗传进化操作后，最终得到相对最优的组合方案，给出题者提供优质的建议，以提高出题效率。

（1）遗传算法简介和应用技术

遗传算法是受自然进化理论启发的一系列搜索算法。通过模仿自然选择和繁殖的过程，遗传算法可以为涉及搜索，优化和学习的各种问题提供高质量的解决方案。同时，它们类似于自然进化，因此可以克服传统搜索和优化算法遇到的一些障碍，尤其是对于具有大量参数和复杂数学表示形式的问题。

（Genetic Algorithm，简称GA）起源于对生物系统所进行的计算机模拟研究，是一种 随机全局搜索优化 方法，它模拟了自然选择和遗传中发生的 复制 、 交叉 (crossover)和变异 (mutation)等现象，从任一初始种群（Population）出发，通过随机选择、交叉和变异操作，产生一群更适合环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代不断繁衍进化，最后收敛到一群最适应环境的个体（Individual），从而求得问题的优质解。

详细参考：https://zhuanlan.zhihu.com/p/436453994

本文使用 PyGad 依赖库（版本：2.19.2），实现 GA 的代码实现，详情使用可参考以下链接：

1. 官方文档：https://pygad.readthedocs.io/en/latest/pygad.html (opens new window)
2. Demo使用：https://zhuanlan.zhihu.com/p/385918911

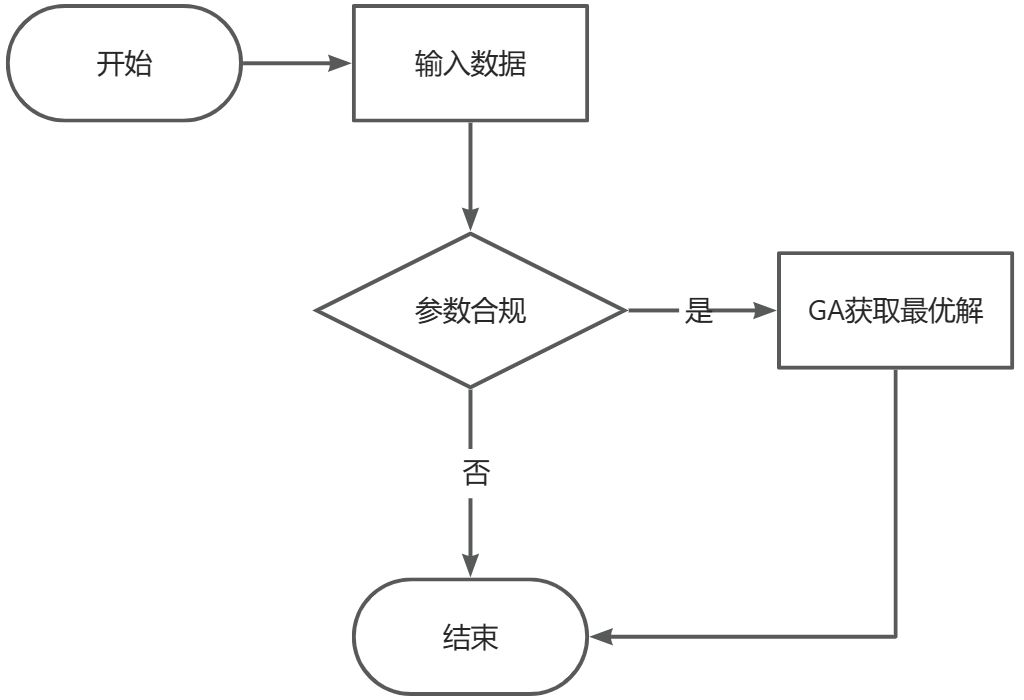
（2）总体思路

(opens new window)

（3）适应度函数设计

1.输入数据

1. questionRange：题目范围：List(index,Question)
2. 1. index：序列号，从0开始
   2. Question：题目信息对象
3. 1. 1. id：题号（int）
      2. tags：知识点标签（list[str]）
      3. questionDifficulty：难度类型（简单（0）、中等（1）、困难（2）,int）
      4. questionType：题目类型（文字题（1）、编程题（0），int）
4. popScore：受众评分(0-5，float)
5. questionNum：题目数量(0,len(questionRange),int)
6. needTags：所需知识点(至多5个,str)
7. typeRate：题目类型比例(文字题:编程题=0:1，int)
8. difficultyRate：题目难度比例（简单:中等:困难=0:1:2，int）

2.函数公式

在构建遗传算法的适应度函数时，我们需要考虑可选题目范围、受众评分、所需知识点、题目类型比例以及题目难度比例等多个因素。

适应度函数公式：

def max_fitness_function(solution, solution_idx):
    # 根据solution索引数组获取题目信息数组
    cur = [questionRange[e] for e in solution]

    # 计算题目类型分布并归一化
    type_distribution = calCurTypeRate(cur)

    # 计算题目难度分布并归一化
    difficulty_distribution = calCurDifficultyRate(cur)

    # 计算题目受众分数
    cur_popScore = calCurPopScore(difficulty_distribution)

    # 计算适应度函数值（公式）
    fitness = (
            weight_popScore * (abs(popScore - cur_popScore) / popScore) +
            weight_tags * calTagsLoss(cur) +
            weight_typeRate * (abs(typeRate[0] - type_distribution[0]) + abs(typeRate[1] - type_distribution[1])) / 2 +
            weight_difficultyRate * sum([abs(difficultyRate[i] - difficulty_distribution[i]) for i in range(3)]) / 3
    )

    return 1.0 / fitness

其中：

1. weight_popScore、weight_tags、weight_typeRate、weight_difficultyRate 是权重系数，用于调整不同参数在适应度函数中的影响程度。这些系数可以根据实际需求进行调整。
2. weight_popScore * (abs(popScore - cur_popScore) / popScore)：受众评分的差异，表示题目与其受众分数和当前方案的受众分数的差距。
3. calTagsLoss(cur)：计算选取的题目中覆盖所需知识点的的比例。通过求交集并除以所需知识点数量（最多5个）来评估知识点覆盖情况。
4. type_distribution：实际选取的题目类型分布比例，需要计算文字题和编程题各自在选取题目中的比例。
5. (abs(typeRate[0] - type_distribution[0]) + abs(typeRate[1] - type_distribution[1])) / 2：计算实际题目类型分布与期望类型分布的差异，取平均值来得到类型分布的差异度。
6. difficulty_distribution：实际选取的题目难度分布比例，需要计算三种难度在选取题目中的比例。
7. sum([abs(difficultyRate[i] - difficulty_distribution[i]) for i in range(3)])：计算实际题目难度分布与期望难度分布的差异，取平均值来得到难度分布的差异度。

（4）其余GA策略和参数

    # pyGad参考链接：https://pygad.readthedocs.io/en/latest/pygad.html#pygad-ga-class
    ga_instance = pygad.GA(
        init_range_low=0,  # 初始种群个体的基因最小值
        init_range_high=len(questionRange) - 1,  # 初始种群个体的基因最大值
        num_generations=50,  # 代数
        num_parents_mating=20,  # 要选择的父母解决方案数量
        parent_selection_type="sss",  # 选择策略（steady_state_selection：稳态选择：保证种群稳定性）
        crossover_type="single_point",  # 交叉策略（单点交叉：适用于二进制编码和实数编码等多种编码方式）
        fitness_func=max_fitness_function,  # 适应度函数
        sol_per_pop=100,  # 每一个种群中个体数量
        num_genes=questionNum,  # 染色体基因的数量
        gene_type=int,  # 基因值的数据类型
        gene_space=range(0, len(questionRange)),  # 基因值的取值范围
        allow_duplicate_genes=False,  # 是否允许染色体中存在重复的值
        mutation_type="random",  # 变异的类型：随机突变
        mutation_percent_genes=5,  # 基因变异的百分比概率
        random_mutation_min_val=0,  # 变异个体的基因最小值
        random_mutation_max_val=len(questionRange) - 1  # 变异个体的基因最大值
    )

（5）完整代码

代码主要包括：

1. GA 各部分的实例代码
2. Flask 的网络接口开发代码

代码地址：https://gitee.com/sspuoj/sspuoj_ai_question_combine/tree/master/online

（6）测试效果

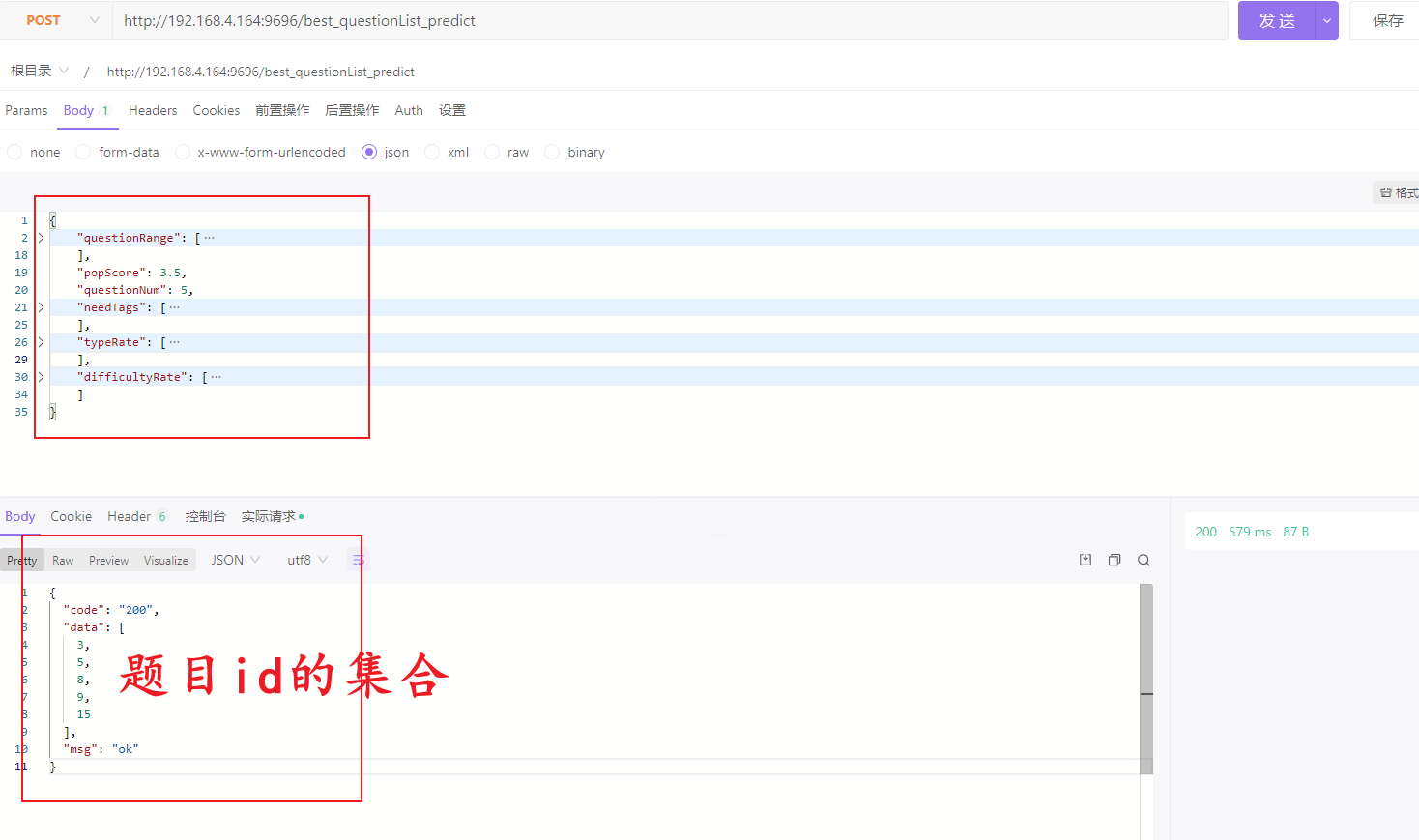
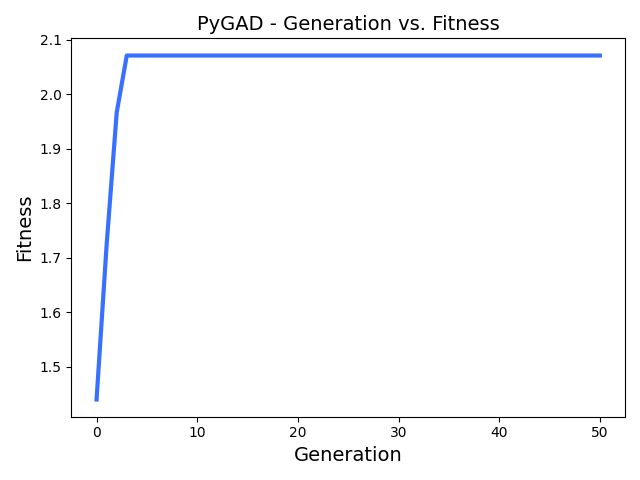
（GA的逐代优化过程变化图）

测试数据：

{
    "questionRange": [
        "{\"questionId\": 1,\"tags\": [\"迭代\", \"递归\"],\"questionType\": 0,\"questionDifficulty\": 0}",
        "{\"questionId\": 2,\"tags\": [\"迭代\", \"DFS\"],\"questionType\": 0,\"questionDifficulty\": 0}",
        "{\"questionId\": 3,\"tags\": [\"迭代\", \"BFS\"],\"questionType\": 1,\"questionDifficulty\": 1}",
        "{\"questionId\": 4,\"tags\": [\"数学\", \"递归\"],\"questionType\": 1,\"questionDifficulty\": 1}",
        "{\"questionId\": 5,\"tags\": [\"前缀和\", \"循环\"],\"questionType\": 0,\"questionDifficulty\": 2}",
        "{\"questionId\": 6,\"tags\": [\"DFS\", \"递归\"],\"questionType\": 1,\"questionDifficulty\": 2}",
        "{\"questionId\": 7,\"tags\": [\"BFS\", \"递归\"],\"questionType\": 1,\"questionDifficulty\": 0}",
        "{\"questionId\": 8,\"tags\": [\"双指针\"],\"questionType\": 0,\"questionDifficulty\": 1}",
        "{\"questionId\": 9,\"tags\": [\"迭代\"],\"questionType\": 0,\"questionDifficulty\": 2}",
        "{\"questionId\": 10,\"tags\": [\"递归\"],\"questionType\": 0,\"questionDifficulty\": 2}",
        "{\"questionId\": 11,\"tags\": [\"迭代\", \"递归\"],\"questionType\": 1,\"questionDifficulty\": 1}",
        "{\"questionId\": 12,\"tags\": [\"迭代\", \"DFS\"],\"questionType\": 1,\"questionDifficulty\": 1}",
        "{\"questionId\": 13,\"tags\": [\"迭代\", \"递归\",\"DFS\"],\"questionType\": 1,\"questionDifficulty\": 0}",
        "{\"questionId\": 14,\"tags\": [\"迭代\", \"递归\",\"BFS\"],\"questionType\": 1,\"questionDifficulty\": 0}",
        "{\"questionId\": 15,\"tags\": [\"迭代\", \"递归\",\"AVL\"],\"questionType\": 1,\"questionDifficulty\": 0}"
    ],
    "popScore": 3.5,
    "questionNum": 5,
    "needTags": [
        "DFS",
        "BFS",
        "递归"
    ],
    "typeRate": [
        0.3,
        0.7
    ],
    "difficultyRate": [
        0.2,
        0.5,
        0.3
    ]
}